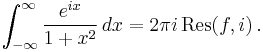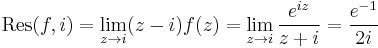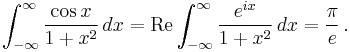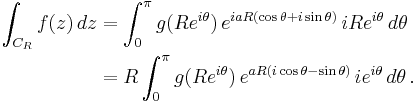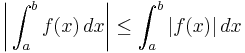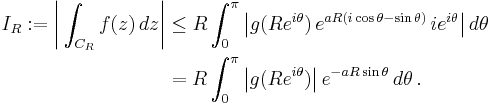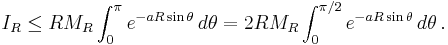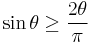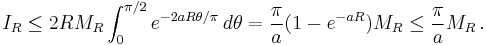Jordan's lemma
In complex analysis, Jordan's lemma is a result frequently used in conjunction with the residue theorem to evaluate contour integrals and improper integrals. The theorem is named after the French mathematician Camille Jordan.
Contents |
Statement
Consider a complex-valued, continuous function f, defined on a semicircular contour
of radius R > 0 lying in the upper half-plane, centred at the origin. If the function f is of the form
with a parameter a > 0, then Jordan's lemma states the following upper bound for the contour integral:
An analogous statement for a semicircular contour in the lower half-plane holds when a < 0.
Remarks
- If f is defined and continuous on the semicircular contour CR for all large R and
- then by Jordan's lemma
- For the case a = 0, see the estimation lemma.
- Compared to the estimation lemma, the upper bound in Jordan's lemma does not explicitly depend on the length of the contour CR.
Application of Jordan's lemma
Jordan's lemma yields a simple way to calculate the integral along the real axis of functions f (z) = eiazg(z) holomorphic on the upper half-plane and continuous on the closed upper half-plane, except possibly at a finite number of non-real points z1, z2, ..., zn. Consider the closed contour C, which is the concatenation of the paths C1 and C2 shown in the picture. By definition,
Since on C2 the variable z is real, the second integral is real:
The left-hand side may be computed using the residue theorem to get, for all R larger than the maximum of |z1|, |z2|, ..., |zn|,
where Res(f, zk) denotes the residue of f at the singularity zk. Hence, if f satisfies condition (*), then taking the limit as R tends to infinity, the contour integral over C1 vanishes by Jordan's lemma and we get the value of the improper integral
Example
The function
satisfies the condition of Jordan's lemma with a = 1 for all R > 0 with R ≠ 1. Note that, for R > 1,
hence (*) holds. Since the only singularity of f in the upper half plane is at z = i, the above application yields
Since z = i is a simple pole of f and 1 + z2 = (z + i)(z - i), we obtain
so that
This result exemplifies how some integrals difficult to compute with classical tools are easily tackled with the help of complex analysis.
Proof of Jordan's lemma
By definition of the complex line integral,
Now the inequality
yields
Using MR as defined in (*) and the symmetry sin θ = sin(π – θ), we obtain
Since the graph of sin θ is concave on the interval θ ∈ [0,π /2], the graph of sin θ lies above the straight line connecting its endpoints, hence
for all θ ∈ [0,π /2], which further implies
See also
References
- Brown, James W.; Churchill, Ruel V. (2004). Complex Variables and Applications (7th ed.). New York: McGraw Hill. pp. 262–265. ISBN 0-07-287252-7.
![C_R=\{z�: z=R e^{i \theta}, \theta\in [0,\pi]\}](/2012-wikipedia_en_all_nopic_01_2012/I/345216ea6cc31a1d7449d2b44359c38e.png)
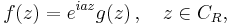
![\biggl|\int_{C_R} f(z)\, dz\biggr| \le \frac\pi{a}\max_{\theta\in [0,\pi]} \bigl|g \bigl(R e^{i \theta}\bigr)\bigr|\,.](/2012-wikipedia_en_all_nopic_01_2012/I/2616561a135e7f676710e031e7b03fdd.png)
![M_R:=\max_{\theta\in [0,\pi]} \bigl|g \bigl(R e^{i \theta}\bigr)\bigr| \to 0\quad \mbox{as } R \to \infty\,,\qquad(*)](/2012-wikipedia_en_all_nopic_01_2012/I/5e0223c295cf6fa8d95a274e20e03c40.png)
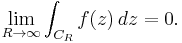
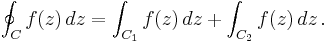
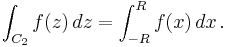
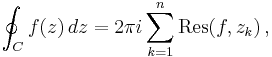
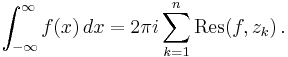
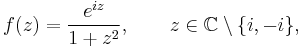
![M_R=\max_{\theta\in[0,\pi]}\frac1{|1%2BR^2e^{2i\theta}|}=\frac1{R^2-1}\,,](/2012-wikipedia_en_all_nopic_01_2012/I/432a9e16c2eb65673210b99b5713698a.png)